Project 3: Inference
Table of contents
- Files
- Introduction
- Getting Started
- Question 1 (3 points) - Exact Inference Observation
- Question 2 (4 points) - Exact Inference with Time Elapse
- Question 3 (3 points) - Exact Inference Full Test
- Question 4 (3 points) - Approximate Inference Observation
- Question 5 (4 points) - Approximate Inference with Time Elapse
- Extra Credit: Question 6 (+1 point) - Joint Particle Filter Observation
- Extra Credit: Question 7 (+2 points) - Joint Particle Filter with Elapse Time
- Debugging Gradescope
- Submission

Files
Download project3.zip via the Canvas assignment page. This zip file contains the following:
| Files you’ll edit and submit | |
bustersAgents.py | Agents for playing the Ghostbusters variant of Pacman |
inference.py | Code for tracking ghosts over time using their sounds |
| Files might want to look at but NOT edit | |
busters.py | The main entry to Ghostbusters (replacing Pacman.py) |
bustersGhostAgents.py | New ghost agents for Ghostbusters |
ghostAgents.py | Agents to control ghosts |
util.py | Utility functions |
distanceCalculator.py | Computes maze distances |
| Supporting files you can ignore | |
autograder.py | Project autograder |
game.py | Inner workings and helper classes for Pacman |
grading.py | Support for project autograder |
graphicsDisplay.py | Graphics for Pacman |
graphicsUtils.py | Support for Pacman graphics |
keyboardAgents.py | Keyboard interfaces to control Pacman |
layout.py | Code for reading layout files and storing their contents |
testParser.py | Parses autograder test and solution files |
testClasses.py | General autograding test classes |
test_cases/ | Directory containing the test cases for each question |
textDisplay.py | Command-line output formatting |
trackingTestClasses.py | Project 3 specific autograding test classes |
Introduction
Pacman spends his life running from ghosts, but things were not always so. Legend has it that many years ago, Pacman’s great grandfather Grandpac learned to hunt ghosts for sport. However, he was blinded by his power and could only track ghosts by their banging and clanging.
In this project, you will design Pacman agents that use sensors to locate and eat invisible ghosts. You’ll advance from locating single, stationary ghosts to hunting packs of multiple moving ghosts with ruthless efficiency.
Imports: Do NOT import any new libraries for this project (ie. numpy, scikit learn, pandas, etc). Some of these libraries trivialize the assignment and importantly they are not installed on the gradescope autograder. Importing these libraries will crash the autograder and that submission will receive a zero. Please also check that your IDE did not incidentally import libraries (common with VSCode for instance). See more in the Debugging Gradescope section.
Evaluation: Your code will be autograded via Gradescope for technical correctness. Please do not change the names of any provided functions or classes within the code, or you will wreak havoc on the autograder. However, the correctness of your implementation – not the autograder’s judgements – will be the final judge of your score. If necessary, we will review and grade assignments individually to ensure that you receive due credit for your work.
Academic Dishonesty: We will be checking your code against other submissions in the class for logical redundancy. If you copy someone else’s code and submit it with minor changes, we will know. These cheat detectors are quite hard to fool, so please don’t try. We trust you all to submit your own work only; please don’t let us down. If you do, we will pursue the strongest consequences available to us.
Getting Help: You are not alone! If you find yourself stuck on something, contact the course staff for help. Office hours, section, and the discussion forum are there for your support; please use them. If you can’t make our office hours, let us know and we will schedule more. We want these projects to be rewarding and instructional, not frustrating and demoralizing. But, we don’t know when or how to help unless you ask.
Discussion: Please be careful not to post spoilers.
Getting Started
In the Pacman version of Ghostbusters, the goal is to hunt down scared but invisible ghosts. Pacman, ever resourceful, is equipped with sonar (ears) that provides noisy readings of the Manhattan distance to each ghost. The game ends when Pacman has eaten all the ghosts. To start, try playing a game yourself using the keyboard.
python busters.py
The blocks of color indicate where the each ghost could possibly be, given the noisy distance readings provided to Pacman. The noisy distances at the bottom of the display are always non-negative, and always within 7 of the true distance. The probability of a distance reading decreases exponentially with its difference from the true distance.
Your primary task in this project is to implement inference to track the ghosts. For the keyboard based game above, a crude form of inference was implemented for you by default: all squares in which a ghost could possibly be are shaded by the color of the ghost. Naturally, we want a better estimate of the ghost’s position. Fortunately, Bayes’ Nets provide us with powerful tools for making the most of the information we have. Throughout the rest of this project, you will implement algorithms for performing both exact and approximate inference using Bayes’ Nets. The project is challenging, so we do encourage you to start early and seek help when necessary.
While watching and debugging your code with the autograder, it will be helpful to have some understanding of what the autograder is doing. There are 2 types of tests in this project, as differentiated by their *.test files found in the subdirectories of the test_cases folder. For tests of class DoubleInferenceAgentTest, you will see visualizations of the inference distributions generated by your code, but all Pacman actions will be preselected according to the actions of the staff implementation. This is necessary in order to allow for a comparison of your distributions with the staff’s distributions. The second type of test is GameScoreTest, in which your BustersAgent will actually select actions for Pacman and you will watch your Pacman play and win games.
As you implement and debug your code, you may find it useful to run a single test at a time. In order to do this you will need to use the -t flag with the autograder. For example if you only want to run the first test of question 1, use:
python autograder.py -t test_cases/q1/1-ExactUpdate
In general, all test cases can be found inside test_cases/q*.
Throughout this project, we will be using the DiscreteDistribution class defined in inference.py to model belief distributions and weight distributions. This class is an extension of the built-in Python dictionary class, where the keys are the different discrete elements of our distribution, and the corresponding values are proportional to the belief or weight that the distribution assigns that element. Take a look at the normalize, sample, and total functions that have been provided.
Question 1 (3 points) - Exact Inference Observation
Your task: Update the observeUpdate method in ExactInference class of inference.py to correctly update the agent’s belief distribution over ghost positions given an observation from Pacman’s sensors.
To run the autograder for this question and visualize the output:
python autograder.py -q q1
As you watch the test cases, be sure that you understand how the squares converge to their final coloring. In test cases where is Pacman boxed in (which is to say, he is unable to change his observation point), why does Pacman sometimes have trouble finding the exact location of the ghost?
If you want to run this test (or any of the other tests) without graphics you can add the following flag:
python autograder.py -q q1 --no-graphics
Note that your busters agents have a separate inference module for each ghost they are tracking. That’s why if you print an observation inside the observeUpdate function, you’ll only see a single number even though there may be multiple ghosts on the board.
Hints:
- You are implementing the online belief update for observing new evidence. Before any readings, Pacman believes the ghost could be anywhere: a uniform prior (see
initializeUniformly). After receiving a reading, theobserveUpdatefunction is called, which must update the belief at every position. - Before typing any code, write down the equation of the inference problem you are trying to solve.
- You should use the function
self.getObservationProbwhich returns the probability of an observation given Pacman’s position, a potential ghost position, and the jail position. You can obtain Pacman’s position usinggameState.getPacmanPosition(), and the jail position usingself.getJailPosition(). - In the Pacman display, high posterior beliefs are represented by bright colors, while low beliefs are represented by dim colors. You should start with a large cloud of belief that shrinks over time as more evidence accumulates.
- Beliefs are stored in a
util.Counterobject (similar to a dictionary) in a field calledself.beliefs, which you should update. - You should not need to store any evidence. The only thing you need to store in
ExactInferenceisself.beliefs.
Question 2 (4 points) - Exact Inference with Time Elapse
In the previous question, you implemented belief updates for Pacman based on his observations. Fortunately, Pacman’s observations are not his only source of knowledge about where a ghost may be. Pacman also has knowledge about the ways that a ghost may move; namely that the ghost can not move through a wall or more than one space in one timestep.
To understand why this is useful to Pacman, consider the following scenario in which there is Pacman and one Ghost. Pacman receives many observations which indicate the ghost is very near, but then one which indicates the ghost is very far. The reading indicating the ghost is very far is likely to be the result of a buggy sensor. Pacman’s prior knowledge of how the ghost may move will decrease the impact of this reading since Pacman knows the ghost could not move so far in only one move.
Your task: Implement the elapseTime method in ExactInference. Your agent has access to the action distribution for any GhostAgent. In order to test your elapseTime implementation separately from your observeUpdate implementation in the previous question, this question will not make use of your observeUpdate implementation.
Since Pacman is not utilizing any observations about the ghost, this means that Pacman will start with a uniform distribution over all spaces, and then update his beliefs according to how he knows the Ghost is able to move. Since Pacman is not observing the ghost, this means the ghost’s actions will not impact Pacman’s beliefs. Over time, Pacman’s beliefs will come to reflect places on the board where he believes ghosts are most likely to be given the geometry of the board and what Pacman already knows about their valid movements.
For the tests in this question we will sometimes use a ghost with random movements and other times we will use the GoSouthGhost. This ghost tends to move south so over time, and without any observations, Pacman’s belief distribution should begin to focus around the bottom of the board. To see which ghost is used for each test case you can look in the .test files.
To run the autograder for this question and visualize the output:
python autograder.py -q q2
As you watch the autograder output, remember that lighter squares indicate that Pacman believes a ghost is more likely to occupy that location, and darker squares indicate a ghost is less likely to occupy that location. For which of the test cases do you notice differences emerging in the shading of the squares? Can you explain why some squares get lighter and some squares get darker?
Hints:
- Instructions for obtaining a distribution over where a ghost will go next, given its current position and the
gameState, appears in the comments ofExactInference.elapseTimeininference.py. - We assume that ghosts still move independently of one another, so you can develop all of your code in this question assuming that only a single ghost exists. The autograder framework will manage several ghosts independently, using your code.
Question 3 (3 points) - Exact Inference Full Test
Now that Pacman knows how to use both his prior knowledge and his observations when figuring out where a ghost is, he is ready to hunt down ghosts on his own. This question will use your observeUpdate and elapseTime implementations together, along with a simple greedy hunting strategy which you will implement for this question. In the simple greedy strategy, Pacman assumes that each ghost is in its most likely position according to its beliefs, then moves toward the closest ghost. Up to this point, Pacman has moved by randomly selecting a valid action.
Your Task: Implement the chooseAction method in GreedyBustersAgent in bustersAgents.py. Your agent should first find the most likely position of each remaining (living/uncaptured) ghost, then choose and return an action that minimizes the distance to the closest ghost. If correctly implemented, your agent should win the game in q3/3-gameScoreTest with a score greater than 700 at least 8 out of 10 times.
Note that the autograder will also check the correctness of your inference directly.
To run the autograder for this question and visualize the output:
python autograder.py -q q3
Hints:
- When correctly implemented, your agent will thrash around a bit in order to capture a ghost.
- The comments of
chooseActionprovide you with useful method calls for computing maze distance and successor positions. - Make sure to only consider the living/uncaptured ghosts, as described in the comments.
Question 4 (3 points) - Approximate Inference Observation
Approximate inference is very trendy among ghost hunters this season. Next, you will implement a particle filtering algorithm for tracking a single ghost.
Your Task: Implement the functions initializeUniformly, getBeliefDistribution, and observeUpdate for the ParticleFilter class in inference.py. A particle (sample) is a ghost position in this inference problem. Note that, for initialization, particles should be evenly (not randomly) distributed across legal positions in order to ensure a uniform prior. When complete, you should be able to track ghosts nearly as effectively as with exact inference.
Note that the variable you store your particles in must be a list. A list is simply a collection of unweighted variables (positions in this case). Storing your particles as any other data type, such as a dictionary, is incorrect and will produce errors. The getBeliefDistribution method then takes the list of particles and converts it into a DiscreteDistribution object.
To run the autograder for this question and visualize the output:
python autograder.py -q q4
Hint: The belief cloud generated by a particle filter will look noisy compared to the one for exact inference.
Question 5 (4 points) - Approximate Inference with Time Elapse
Your Task: Implement the elapseTime function for the ParticleFilter class in inference.py. This function should construct a new list of particles that corresponds to each existing particle in self.particles advancing a time step, and then assign this new list back to self.particles. When complete, you should be able to track ghosts nearly as effectively as with exact inference.
Note that in this question, we will test both the elapseTime function in isolation, as well as the full implementation of the particle filter combining elapseTime and observeUpdate.
To run the autograder for this question and visualize the output:
python autograder.py -q q5
Extra Credit: Question 6 (+1 point) - Joint Particle Filter Observation
So far, we have tracked each ghost independently, which works fine for the default RandomGhost or more advanced DirectionalGhost. However, the prized DispersingGhost chooses actions that avoid other ghosts. Since the ghosts’ transition models are no longer independent, all ghosts must be tracked jointly in a dynamic Bayes net!
The Bayes net has the following structure, where the hidden variables G represent ghost positions and the emission variables E are the noisy distances to each ghost. This structure can be extended to more ghosts, but only two (a and b) are shown below.
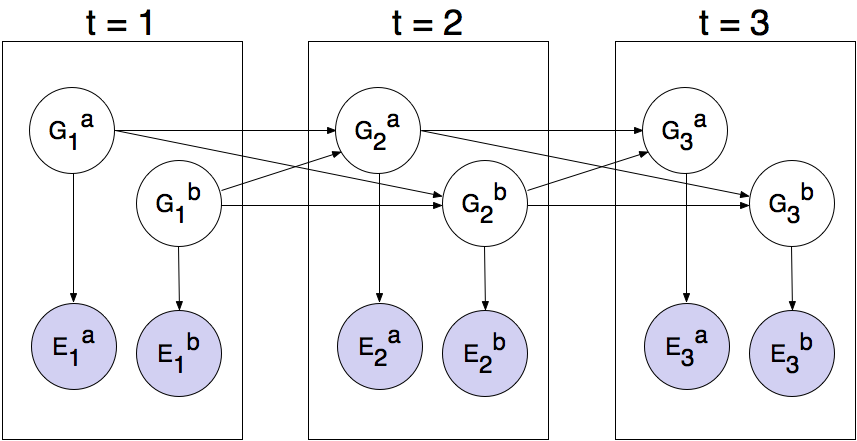
You will now implement a particle filter that tracks multiple ghosts simultaneously. Each particle will represent a tuple of ghost positions that is a sample of where all the ghosts are at the present time. The code is already set up to extract marginal distributions about each ghost from the joint inference algorithm you will create, so that belief clouds about individual ghosts can be displayed.
Your Task: Complete the initializeUniformly and observeUpdate methods in JointParticleFilter to weight and resample the whole list of particles based on new evidence. Your initialization should be consistent with a uniform prior. You may find the Python package itertools useful. Specifically, look at itertools.product to get an implementation of the Cartesian product. However, note that, if you use this, the permutations are not returned in a random order. Therefore, you must then shuffle the list of permutations in order to ensure even placement of particles across the board. As before, use self.legalPositions to obtain a list of positions a ghost may occupy. Also as before, the variable you store your particles in must be a list. Your implementation should also again handle the special case when all particles receive zero weight.
Read the comments in the function for useful hints.
You should now effectively track dispersing ghosts. To run the autograder for this question and visualize the output:
python autograder.py -q q6
Extra Credit: Question 7 (+2 points) - Joint Particle Filter with Elapse Time
Your Task: Complete the elapseTime method in JointParticleFilter in inference.py to resample each particle correctly for the Bayes net. In particular, each ghost should draw a new position conditioned on the positions of all the ghosts at the previous time step. The comments in the method provide instructions for support functions to help with sampling and creating the correct distribution.
Note that completing this question involves removing the call to util.raiseNotDefined(). This means that the autograder will now grade both question 6 and question 7. Since these questions involve joint distributions, they require more computational power (and time) to grade, so please be patient!
As you run the autograder note that q7/1-JointParticlePredict and q7/2-JointParticlePredict test your elapseTime implementations only, and q7/3-JointParticleFull tests both your elapseTime and observeUpdate implementations. Notice the difference between test 1 and test 3. In both tests, Pacman knows that the ghosts will move to the sides of the gameboard. What is different between the tests, and why?

To run the autograder for this question use:
python autograder.py -q q7
Heads Up: this question will take a long time to run.
Congratulations! Only one more project left.
Debugging Gradescope
Once you’ve run your code using the local autograder and are happy with your score, it’s time to submit your assignment! When you upload your code to Gradescope, you will hopefully see the same exact score you saw locally. But sometimes you’ll see something like this:
The autograder failed to execute correctly. Contact your course staff for help in debugging this issue. Make sure to include a link to this page so they can help you most effectively.
If your code runs fine locally, but you see this error on Gradescope, then it is most likely an issue of imports. Check your imports in bustersAgents.py. They should look like:
import util
from game import Agent
from game import Directions
from keyboardAgents import KeyboardAgent
import inference
import busters
Check your imports in inference.py. They should look like:
import itertools
import random
import busters
import game
from util import manhattanDistance, raiseNotDefined
import util
Remember, you are not allowed to import any other libraries for this assignment. Remove those library imports and update your code so that it doesn’t rely on them.
If you didn’t try importing any other packages, then it’s possible that you’re using the wrong version of Python locally, or that you used some sort of obscure python feature that the autograder can’t handle. The autograder runs using Python 3.10; make sure that you’re testing locally using Python 3.x.
If you still can’t figure out why the autograder won’t run, then please send a message to the course staff.
Submission
You’re not done yet! Submit ONLY the following files to Project 3 on Gradescope:
bustersAgents.pyinference.py