Owing to the vast complexity of visual stimuli, perceptual organization is considered an esseintial step in biological visual processing, and nowadays, perhaps more than ever, in computational vision as well. In my research I have been concentrating on computational perceptual organization with an additional emphasis on phychophysics and neuro-physiology. While most research in perceptual organization deals with curve integration, I concentrate on a somewhat neglagted structure which is sometimes called texture flow - a class of visual patterns characterized by local parallelism and almost everywhere local dominant orientation. These structures are interesting from the point of view of perceptual organization both on their own and in relation to their interaction with curves. Furthermore, they are equaly important to other fields of computer vision, such as shading or motion analysis.

1. Computational modeling of texture flow and its good continuation

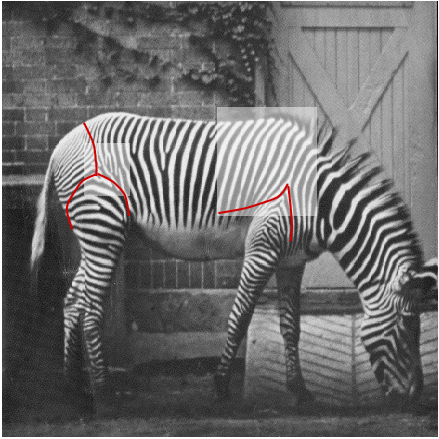Unfortunately, existing computational approaches to the analysis of texture flows, such as fitting or diffusion, ignore certain aspects of their structure. As a result, the processed flow may be distorted, especially around certain kind of discontinuities (e.g., see the orientation diffusion failure in the synthetic flows demos). Furthermore, the fact that coherent flow may contain a wide range of orientations within a small area takes its toll on segmentation methods leading to results that may disagree with perception. Typically, such problems occur around orientatoin singularities such as the one on the back of the zebra. (Figure on the right shows a typical segmentation lines around the zebra's singularities as computed by the normalized-cut algorithm).

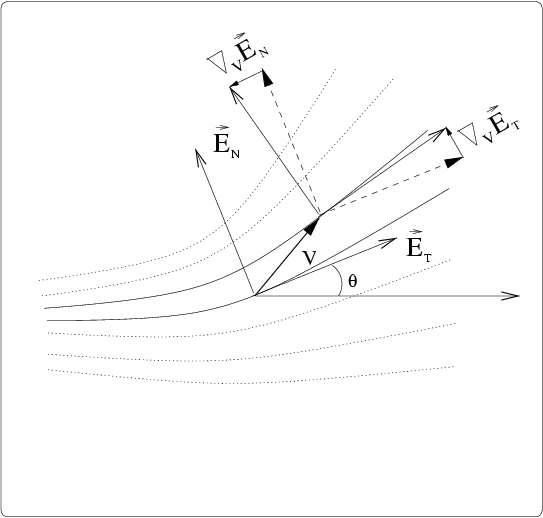In order to avoid these problems, we analyzed texture flows to reveal the parameters that may govern their coherence. Using the frame field representation (Fig. on the left), an object-centered view of the local behavior of texture flows is expressed in terms of the covariant derivative of the underlying pattern. Since the covariant derivatives are vectors, they can be expressed in terms of the frame ifself, which serves as a basis. The result leads to the connection equation and eventually to two scalars that represent the local behaviot of the flow in a flow-centered way. We call the tangential curvature and the normal curvature of the underlying pattern because they describe the rate of change of the flow's dominant orientation in two natural directions.

Since the local behavior of the flow is characterized (up to Euclidean transformation) by a pair of curvatures, it is natural to conclude that nearby local measurements of texture flow orientation should relate to each other based on these curvatures. Put differently, measuring a particular curvature pair at a point q q . Clearly, that field, which we call the texture flow osculating object , should be a function of the local curvatures. Once such an object is designed, coherence of local measurements of texture flow can then be determined in a manner analogous to cocircularity for tangents to a curve via the osculating circle. Much of our computational work was to design such an osculating object that will reflect both good continuation and will not bias one curvature over the other (and interestingly, there is a single such object). The result was an object that takes the shape of a right helicoid in the space R²xS¹ (Figure on the right). With such a prototypical model, coherence of nearby flow patches can be determined by transporting one of them along its corresponding helicoid and checking the alignment of the result with the second flow patch.

Additional reading

• O. Ben-Shahar and S.W. Zucker, The Perceptual Organization of Texture Flow: A Contextual Inference Approach, IEEE Transaction on Pattern Analysis and Machine Intelligence, 25(4) 401-417, 2003.
  
  
• O. Ben-Shahar and S.W. Zucker (2001), On the Perceptual Organization of Texture and Shading Flows: From a Geometrical Model to Coherence Computation , In the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, , Hawaii, December 2001.
  
  
• O. Ben-Shahar and S.W. Zucker (2001), Flowing towards coherence: On the geometry of texture and shading flow , The third workshop on Perceptual Organization in Computer Vision, Vancouver, Canada, July 2001.
  
  

2. The computational perceptual organization of texture and shading flows

The advantage of having a model for the local behavior of a "good" texture flow lies in the ability to assess the degree to which a particular measurement is compatible, or consistent, with the context in which it is embedded. This, in turn, can be used to refine noisy measurements, remove spurious ones, and fill in ``holes'' so that local ambiguity is reduced and global structures become coherent.

A natural framework with which one can pursue this task while maximizing the average consistency over a domain of interest is {\em relaxation labeling}. We developed such a relaxation network for the organization of coherent texture flows and derived the compatibility function which governs its behavior from the right helicoidal model. In addition to handling both dense (right image) and sparse data (left image), and stability over discontinuities and singularities both in orientaiton and curvature, our approach is able to deal with multiple orientations at a point, thus supporting overlapping textures (say, via transparency) and textures of more ethan one dominant orientation at each point. Significant improvement over previous approaches is also the fact that non coherent structures are not "refined" into coherent ones but rather rejected as being non flows. Few of these features are demontrated by the two examples on the right and the left (click the image to see relaxation in action). Note, in particular, how the region of the knot is quickly rejected (i.e., labeled as non-flow), how the singularity in the fingerprint dataset is well preserved, and how the spurious measurements in both images are eliminated and replaced by coherent ones, To see an large set of examples, both for synthetic and natural flows (texture and shading), go to the Demos page.

Additional reading

• O. Ben-Shahar, P. Huggins, and S.W. Zucker (2002), On Computing Visual Flows with Boundaries: The Case of Shading and Edges, In the 2nd Workshop on Biologically Motivated Computer Vision, Tüubingen, Germany, November 2002.
  
  
• O. Ben-Shahar and S.W. Zucker, The Perceptual Organization of Texture Flow: A Contextual Inference Approach, IEEE Transaction on Pattern Analysis and Machine Intelligence, 25(4) 401-417, 2003.
  
  
• O. Ben-Shahar and S.W. Zucker (2001), On the Perceptual Organization of Texture and Shading Flows: From a Geometrical Model to Coherence Computation , In the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, , Hawaii, December 2001.
  
  

3. Curvatures vs. gradient in orientation-based segmentation

Texture segregation has long been attriuted to changes in the distribution of elementary features across the visual fields. Interestingly, orientation has been always considered of prime importance and thus the link between the computational modeling discussed above and orientation-based texture segmentation has become of fundamental interest to us. While contemporary model for orientation-based segmentation depend only on one or two orientation gradients, it is in fact possible to show that these models are at best partial. For example, the stimulus on the right has a constant orientation gradient both within the figure (a square) and the ground, and a constant orientation contrast between them. Nevertheless, the saliency of the square is anything but constant along it's boundary. To check other related perceptual demos check my demos page.

Based on our geometrical analysis and the identification of two texture flow curvatures we hypothesized that these curvatures, and their discontinuities are an important factor in orientation-based segmentation. We have been conducting psychophysical experiments to verify this conjecture and the results suggest that performance of orientation-based curvature peaks when the texture flow undergoes discontinuity in both curvatures along the orientation edge. For example, the graph on the left shows segmentation accuracy for a figure/ground segmentation task where the orientation gradient within the figure and the ground were constant at 15 degrees/unit distance, and the orientation contrast between them varried from 54 degrees to 90 degrees. For each such case we manipulated the orientation field such that the discontinuities in curvatures behave differently (although, again, the two orientation gradients remain fixed). It can be seen that one of the graphs (the green) indicates a qualitatively better performance relative to the others. It is left to conclude that orientation gradients alone cannot explain this result.

The possible implications of these results may be very significant. In particular, since the notion of feature gradient is fundamental not only to orientation, these results justify an inquiry into the intrinsic geometry of other perceptual features like shading, motion, and color.

Additional reading

• O. Ben-Shahar and S.W. Zucker, Sensitivity to Curvature Revealed in Orientation-Based Texture Segmentation, Vision Research (In Press).
  
  
• O. Ben-Shahar and S.W. Zucker (2002), Curvature and the Perceptual Organization of Texture Flows , Annual meeting of the Vision Science Society, Sarasota, Florida, May 2002.
  
  

4. Texture flow and attention

It is now well established that the units of attention are not spatial only but rather relate to perceptual objects in the visual field. While much work in the field of object-based attention is aimed at finding these units, the relationship to basic features that guide segmentation (which is, after all, a mechanism that defines objects) is largly unexplored.

Joining forces with Brian Scholl, an expert in object based attention from the department of Psychology at Yale, we attempt to address this issue while exploiting the theoretical understanding we now have about texture flows. Since the theory of texture flow good continuation suggests clear criteria for segmentation, we seek to put these criteria to test through experimentation with the speard of attention.

More to come about our progress in the near future...

5. Geometry and the projection pattern of long range horizontal connections in V1

Neurons in primary visual cortex respond selectively to oriented stimuli such as edges and lines. The long-range horizontal connections between them are thought to facilitate contour integration. While many physiological and psychophysical findings suggest that colinear or association-field models of good continuation dictate particular projection patterns of horizontal connections to guide this integration process, significant evidence of interactions inconsistent with these hypotheses is accumulating. For examples facilitory interaction between cells of significant orientation difference, short range co-axial inhibition, iso-orientation side facilitation, and strong correlations between iso-oriented, non-overlapping, and parallel receptive fields are functionally inconsistent. Evidence of cross-orientation and non-axial connections, plus roughly isotropic retinotopic extent, suggest anatomical inconsistencies.

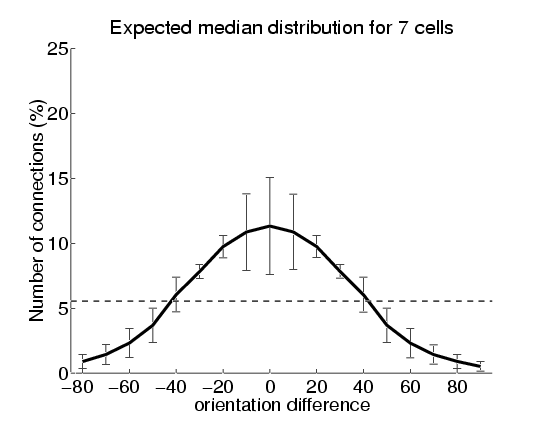
A closer examination of the interactions within visual cortex and their population statistics, and in particular the now increasingly more accurate statistics about the distribution of connections in the orientation domain (e.g., through registeration of optical images and axon terminal distributions obtained with extracellular injected markers; see the image on the right from [Bosking etal. 1997]), suggests that individual cells may have qualitatively different connectivity distributions: some are narrow and high while others are very wide . When averaged, the pooled distribution is (i) unimodal, (ii) peaks at zero orientation offset, (iii) indicates a non-negligible fraction of connections linking cells of significantly different orientation preferences, and (iv) crosses the uniform distribution at approximately $\pm 40$ degrees . Unfortunately, neither colinearity nor association field models predicts all of these features. While both models imply unimodal pooled distributions over orientation differences, neither predicts differences between the distributions of individual cells. Furthermore, quantitative representation if colinearity show that it is clearly at odds with the significant spread in the measured distribution of connections over orientation differences.

It is tempting to explain these apparent anomalies as random physiological variations, but such an examination reveals that even an overwhelming amount of noise fails to predict the measured features (and in particular, the non-monotonic variance). However, the long range connections are commonly believed to integrate information based on good continuation. Since we have analyzed good continuation computationally , we examined the predictions about connectivity patterns from the computational model developed above and compared them to the neuro-anatomical data about the connectivity patterns of long range horizontal interactions between striate receptive fields. One set of comparisons is demonstrated in the image to the right . The computational model predicts significant differences between cells and shows a striking match between the computational and biological data, not only for the pooled distributions, but for their second order statistics (variance) as well.

.

Additional reading

• O. Ben-Shahar and S.W. Zucker, Geometrical Computations Explain Projection Patterns of Long Range Horizontal Connections in Visual Cortex, Neural Computation (In Press).
  
  

6. A perceptual organization approach to denoising color images

The denoising of color images is an increasingly studied problem whose state-of-the-art solutions employ a variety of diffusion schemes. Specifying the correct diffusion is difficult, however, in part because of the subtleties of color interactions. We address this difficulty by proposing a perceptual organization approach to color denoising that treats explicitly two observations, that (1) the color is typically piecewise smooth over the image, and (2) that it may vary greatly, albeit smoothly, even within perceptually coherent objects. The second observation is most vivdly illustrated in the figure above which shows how the hues changes smoothly across the apple, single object present. The 3D plot shows the hue as a surface in R²xS¹ (click to see larger images).

In taking this approach, at this point we focus on the periodic chromatic (hue) component of the color in its representation as a unit length vector field. This allows a purely geometrical considertion and transform color to an instance of...texture flow , or what we call the hue field . The hue field represents the geometrical content of the perceptual dimension of the color suggest the existence of two hue curvatires , and a good continuation contextual approach for the organization of coherent, even if varying, color patches. Again, we emply the right helicoidal model, although this time in the range [-Pi,pi), and adapt our relaxation labeling approach to deal with color (At this point we treat the two other scala chanels (saturation and lightness) with anisotropic diffusion. However, an integrated good continuation approach is on its way...). The result is a robust noise removal process that preserves discontinuities, singularities, and fine chromatic structures, including those that diffusion processes are prone to distort. Two examples are shown on the left. Click the noisy image to see the noise removal proces in action (animation files may be big. Please be patient). For more examples check the Demos page.

Additional reading

• O. Ben-Shahar and S.W. Zucker, Hue Fields and Color Curvatures: A Perceptual Organization Approach to Color Image Denoising, In the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Wisconsin, June 2003.