Problem : Write negations of the following sentences.
- Prof. Glenn is a bad player but he can make free throws. Either Prof. Glenn isn't a bad player or he can't make free throws.
- If Burt drives a Camaro then Candy likes Burt. Burt drives a Camaro but Candy doesn't like him.
- Everyone who lives on the 17th floor is wealthy. Someone who lives on the 17th floor is not wealthy.
- All dairy farmers have a machine that can milk any cow. Some dairy farmer's machines all fail to milk some cow.
Problem : Let $L(x, y)$ be the predicate "$x$ lives in $y$". Let $S(x, y)$ be the predicate "$x$ shops at $y$". Let the domains of the variables and the truth of the predicates for particular values be as indicated by the tables given below. Use $P$ for the set of people, $C$ for the set of cities (ignoring the fact that Columbia and Timonium are Census Designated Places, not cities), and $S$ for the set of stores.
| $L$ | $S$ | |||||
| Clinton | Branford | Trumbull | Aldi | Wegmans | Shoprite | |
|---|---|---|---|---|---|---|
| Chidi | ✓ | ✓ | ✓ | |||
| Eleanor | ✓ | ✓ | ✓ | |||
| Tahani | ✓ | ✓ | ✓ | |||
| Jason | ✓ | ✓ | ||||
| Janet | ✓ | ✓ | ||||
Write each of the following English statements symbolically and determine whether they are true or false. Explain your answers briefly.
- Chidi shops at Aldi.
$S(Chidi, Aldi)$ – true
- Everyone who lives in Clinton shops at Aldi.
$\forall x \in P, L(x, Clinton) \rightarrow S(x, Aldi)$ – true since Chidi, Eleanor, and Tahani are the only Clinton residents and all shop at Aldi.
- No one shops at two different stores.
$\forall x \in P, \forall s_1, s_2 \in S, S(x, s_1) \wedge S(x, s_2) \rightarrow s_1 = s_2$ – false since Eleanor shops at both Aldi and Wegmans.
- There is a store whose patrons all live in Clinton.
$\exists s \in S, \forall x \in P, S(x, s) \rightarrow L(x, Clinton)$ – true since the only patron of Wegmans (Eleanor) lives in Clinton.
- There is a place whose residents all shop at the same store.
$\exists c \in C, \exists s \in S, \forall p \in P, L(p, c) \rightarrow S(p, s)$ – true since all residents of Clinton shop at Aldi.
Problem : Prove or disprove: for any integers $a$, $b$, $c$, and $d$, if $a + b \mid d$ and $a + c \mid d$ then $b + c \mid d$.
Counterexample: let $a = 2$, $b = 0$, $c = 3$, $d = 10$. Now $2 + 0 \mid 10$ and $2 + 3 \mid 10$ but $0 + 3 \not\mid 10$.
Problem : Find an integer $r$ such that $0 \le r \le 12$ and $11^8 \equiv r \pmod{13}$.
$11^8 \equiv (-2)^8 \equiv \left( {(-2)^4} \right) ^2 \equiv 16^2 \equiv 3^2 \equiv 9 \pmod{13}$
Problem : Find the smallest $k$ such that any amount of at least $k$ cents can be made with 4-cent and 5-cent stamps. Prove your answer.
$k = 12$ works.
Base cases (k = 12, 13, 14, 15): In all cases, there exist nonnegative integers $a$ and $b$ so that $k = 4a + 5b$: for 12, let $a=3$ and $b=0$ ($12 = 3 \cdot 4$); for 13, let $a=2$ and $b=1$ ($13 = 2 \cdot 4 + 5$); for 14, let let $a=1$ and $b=2$ ($14 = 4 + 2 \cdot 5$); and for 15, let $a=0$ and $b=3$ ($15 = 3 \cdot 5)$.
Inductive step: Let $k \ge 16$ and suppose any amount from 12 cents to $k-1$ cents can be made with 4- and 5-cent stamps. Then, since $12 \le k-4 \le k$ because $k \ge 16$, the inductive hypothesis says $k-4$ cents can be made with 4- and 5-cent stamps. Let $a$ and $b$ be the number of 4- and 5-cent stamps used to make $k-4$ cents (so $k-4 = 4a + 5b$ and $a,b \in \mathbb{N}$). Now $k$ cents can be made with $a+1$ 4-cent stamps and $b$ 5-cent stamps ($k = k-4+4 = 4a+5b+4 = 4(a+1)+5b$, where $a+1\in \mathbb{N}$ because $a,1\in \mathbb{N}$ and $\mathbb{N}$ is closed under addition).
Problem : Define a sequence by $d_1=3$ and $d_k = 6 \cdot d_{n-1} + 2$ for $n \ge 2$. Find an explicit formula for $d_n$.
We guess the general form \begin{eqnarray} d_n & = & 6^{n-1} \cdot 3 + \sum_{i=0}^{n-2} (6^i \cdot 2) \cr & = & 6^{n-1} \cdot 3 + 2 \cdot \sum_{i=0}^{n-2} 6^i \cr & = & 6^{n-1} \cdot 3 + 2 \cdot {6^{n-2+1} -1 \over 6-1} \cr & = & 6^{n-1} \cdot 3 + 2 \cdot {6^{n-1} -1 \over 5} \cr & = & {17 \over 5} \cdot 6^{n-1} - {2 \over 5} \cr \end{eqnarray}
We could prove that our formula is correct by induction, but for now we will merely check the first few terms: $d_1 = 3, d_2 = 20, d_3 = 122$ and ${17 \over 5} \cdot 1 - {2 \over 5} = 3$, ${17 \over 5} \cdot 6 - {2 \over 5} = 20$, ${17 \over 5} \cdot 36 - {2 \over 5} = 122$.
Problem : Define a sequence by $c_0 = 8$, $c_1 = 21$ and $c_k = 5 \cdot c_{k-1} - 6 \cdot c_{k-2}$ for $k \ge 2$. Find an explicit formula for $c_n$.
The recurrence is in the form $c_k = Ac_{k-1} + Bc_{k-2}$ where $A=5$ and $B=-6$ so we use the method of solving second-order linear homogeneous recurrences with constant coefficients. First, solve the characteristic equation $t^2 - At - B = 0$ which in this case is $t^2 - 5t + 6 = 0$, which has roots $r=2$ and $s=3$. So we know the formula is in the form $c_n = C \cdot 2^n + D \cdot 3^n$. We use the initial terms to solve for $C$ and $D$: \begin{eqnarray} c_0 & = & C \cdot 2^0 + D \cdot 3^0 \cr 8 & = & C + D \cr \end{eqnarray} \begin{eqnarray} c_1 & = & C \cdot 2^1 + D \cdot 3^1 \cr 21 & = & 2C + 3D \cr \end{eqnarray}
Which yields $C=3$ and $D=5$. So the formula is $c_n = 3 \cdot 2^n + 5 \cdot 3^n$. Again, a formal proof that the formula is correct would use induction but here we merely check a few terms: $c_0 = 8$, $c_1 = 21$, $c_2 = 57$ and $3 \cdot 2^0 + 5 \cdot 3^0 = 8$, $3 \cdot 2^1 + 5 \cdot 3^1 = 3 \cdot 2 + 5 \cdot 3 = 21$, and $3 \cdot 2^2 + 5 \cdot 3^2 = 3 \cdot 4 + 5 \cdot 9 = 57$.
Problem : Prove that for any sets $A$ and $B$, $A \cup (A \cap B) = A$ using no properties of sets other than the definitions of the set operations.
Let $x \in A \cup (A \cap B)$. Then either $x \in A$ or $x \in A \cap B$ by definition of $\cup$. In the former case we immediately have $x \in A$. In the latter case, $x \in A$ and $x \in B$ by definition of $\cap$. So in either case $x \in A$. Therefore $A \cup (A \cap B) \subseteq A$.
Let $x \in A$. Then $x \in A \vee x \in A \cap B$, so by definion of $\cup$, $x \in A \cup (A \cap B)$. Therefore $A \subseteq A \cup (A \cap B)$.
Since $A \cup (A \cap B) \subseteq A$ and $A \subseteq A \cup (A \cap B)$, $A = A \cup (A \cap B)$.
Problem : Prove that, for any sets $A$, $B$, $C$, and $D$, if $C \subseteq A-B$ and $D \subseteq B-A$ then $C$ and $D$ are disjoint.
Problem : Prove or disprove: for any sets $A$ and $B$, ${\cal P}(A-B) = {\cal P}(A) - {\cal P}(B)$.
Problem : A state issues license plates in two formats: either two letters followed by three numbers, or 5 numbers with a letter somewhere between them (but not at the ends). How many different license plates can the state issue?
Problem : Imagine a game like poker but played with 4 card hands. Which should be a better hand: one pair or ``melting pot'', which is four cards all of different ranks and different suits (that is, which is less likely to be made from a randomly dealt hand of 4 cards)?
There are fewer than $13 \cdot 12 \cdot 11 \cdot 10 = 17160$ melting pot hands (choose the rank of the spade, the rank of the heart, the rank of the diamond, and the rank of the club; this total includes some straights hence the qualifier "fewer than"). So melting pot should beat one pair.
Problem : 50 people were surveyed about what TV shows they watch. 21 reported that they watch The Amazing Race, 25 watch Veronica Mars, and 11 watch Arrested Development. 3 watch AD and TAR, 9 watch TAR and VM, 3 watch VM and AD, and 1 watches all 3. Fill in the Venn diagram that shows how many people watch each possible combination of shows.
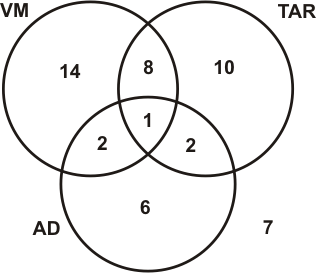
Problem : 12 people are to be seated for a jury. The jury pool consists of 20 people: 7 college students, 10 retirees, and 3 working professionals.
- How many possible juries are there?
${20 \choose 12}$ - How many have an equal number from each group?
None have an equal number from each group since there aren't enough working professionals. - How many include no retirees?
None include no retirees because there aren't enough non-retirees. - How many include at most 3 retirees?
We need to least 2 retirees in order to get to 12 total; split this into juries with 2 retirees and with 3 retirees: ${10 \choose 2} + {10 \choose 3} \cdot {10 \choose 9}$ - How many include all the college students?
${13 \choose 5}$ - How many include more working professionals than college students?
${7 \choose 2} \cdot {10 \choose 7}$ include 3 working professionals and 2 college students, ${7 \choose 1} \cdot {10 \choose 8}$ include 3 professionals and 1 college student, ${10 \choose 9}$ include 3 professionals and no college student, ${3 \choose 2} \cdot {7 \choose 1} \cdot {10 \choose 9}$ include 2 professionals and 1 college student, and ${3 \choose 2}$ include 2 professionals and no college students, for a total of $ {7 \choose 2} \cdot {10 \choose 7} +{7 \choose 1} \cdot {10 \choose 8} +{10 \choose 9} +{3 \choose 2} \cdot {7 \choose 1} \cdot {10 \choose 9} +{3 \choose 2} $ with more professionals than college students.
Problem : The game Can't Stop is played with 4 indistinguishable 6-sided dice. How many distinct outcomes are there of rolling the dice?
Problem : Define $f: {\bf R} \rightarrow {\bf R}$ by $f(x) = (x - 1)(x + 2)(x + 3)$. Is $f$ 1-1? Is $f$ onto? Explain your answers.
Problem : Define $f:\{0,1\}^* \rightarrow {\bf Z}$ by $f(s) = $the length of the longest sequence of 0's in $s$ (so, for example, $f(00000) = 5$, $f(11001) = 2$ and $f(111) = 0$). Is $f$ 1-1? Is $f$ onto? Explain your answers.
Problem : Is the set of nondecreasing functions from $\mathbb{N}$ to $\{0, 1, \ldots, 99\}$ countable or uncountable? Justify your answer.
Problem : Is the set of nondecreasing functions from $\mathbb{N}$ to $\mathbb{N}$ countable or uncountable? Justify your answer.
Problem : Consider the relation $R$ on ${\bf Z^+}$ defined by $xRy$ if and only if $gcd(x,y) \gt 1$.
- Is $R$ reflexive? Explain your answer.
- Is $R$ symmetric? Explain your answer.
- Is $R$ antisymmetric? Explain your answer.
- Is $R$ transitive? Explain your answer.
- Is $R$ an equivalence relation?
- Is $R$ a partial order?
- Is $R$ a total order?
$R$ is not reflexive since $gcd(1,1) = 1$ and $1 R 1$ is false.
$R$ is symmetric since if $x R y$ then $gcd(x,y) \gt 1$ and $gcd(y,x) = gcd(x,y) \gt 1$ and therefore $y R x$.
$R$ is not antisymmetric since $gcd(8,2) = gcd(2,8)=2$ and so $2R8$ and $8R2$ but $2 \ne 8$.
$R$ is not transitive: $2 R 6$ and $6 R 3$ are both true but $2 R 3$ is false.
$R$ is not an equivalence relation because it is neither reflexive nor transitive.
$R$ is not an partial because it is neither reflexive nor antisymmetric, nor transitive.
$R$ is not a total order because it is not a partial order.
Problem :
Consider the relation $S$ defined on finite-length strings of letters
a,...,z defined by $xSy$ if and only if $x$ is a substring of $y$
(in Java terms, if there are integers a and b
so that y.substring(a,b).equals(x)).
- Is $S$ reflexive? Explain your answer.
- Is $S$ symmetric? Explain your answer.
- Is $S$ antisymmetric? Explain your answer.
- Is $S$ transitive? Explain your answer.
- Is $S$ an equivalence relation?
- Is $S$ a partial order?
- Is $S$ a total order?
$S$ is reflexive: for any string $x$, $x$ is a substring of itself, so $xSx$.
$S$ is not symmetric: "be" is a substring of "bear" but "bear" is not a substring of "be".
$S$ is antisymmetric: if $xRy$ and $x \ne y$, then $y$ must be longer than $x$. But then $y$ can't be a substring of $x$, so it is not the case that $ySx$.
$S$ is transitive: suppose $x$ is a substring of $y$
and $y$ is a substring of $z$.
Then there is an $a$ and $b$ such that y.substring(a,b).equals(z)
and a $c$ and $d$ such that z.substring(c,d).equals(y).
But then z.substring(c+a, c+b).equals(x), so $x$ is a substring of $z$.
$S$ is not an equivalence relation because it is not symmetric.
$S$ is a partial order because it is reflexive, antisymmetric, and transitive.
$S$ is not a total order because there are strings that are not comparable: for example, $baltimore$ is not a substring of $orioles$ and $orioles$ is not a substring of $baltimore$.
Problem : Consider the relation $T$ defined on ${\bf Z}_{10} = \{0,1,2,3,4,5,6,7,8,9\}$ defined by $xTy$ if and only if $3|(x^3-y^3)$. Show that $T$ is an equivalence relation and give the corresponding equivalence classes.
$T$ is reflexive: let $x \in {\bf Z}_{10}$. Then $x^3 -x^3 = 0$ and $3 | 0$ so $xTx$.
$T$ is symmetric: let $x,y \in {\bf Z}_{10}$ and suppose $xTy$. Then by definition of $T$, $3|(x^3-y^3)$ and by properties of divisibility $3 | (y^3-x^3)$ (use $a|b \wedge m\in{\bf Z} \Rightarrow a|bm$ with $a=3$, $b=(x^3-y^3)$ and $m=-1$). So $yTx$.
$T$ is transitive: let $x,y,z \in {\bf Z}_{10}$ and suppose $xTy$ and $yTz$. The by definition of $T$ we have $3|(x^3-y^3)$ and $3|(y^3-z^3)$. Now by properties of divisibility we have $3|(x^3-z^3)$ so $xTz$ (use $a|b \wedge a|c \Rightarrow a|(b+c)$ with $a=3$, $b = x^3-y^3$ and $c=y^3-z^3$).
The equivalence classes are $[0] = \{0, 3, 6, 9\}$, $[1] = \{1, 4, 7\}$ and $[2] = \{2, 5, 8\}$.
Problem : Let $\preccurlyeq$ be a partial order on a set $S$. Let $R$ be the relation defined by $xRx$ for all $x \in S$ and $xRy$ when $y \preccurlyeq x$ and $x \ne y$. What can you say about $R$?
$R$ is reflexive because by definition, $xRx$ for all $x \in S$.
$R$ is also antisymmetric, for suppose by way of contradiction, that $xRy$ and $yRx$ for some $x, y \in S$ with $x \ne y$. Then, by definition of $R$, we have $y \preccurlyeq x$ and $x \preccurlyeq y$. So $\preccurlyeq$ is not antisymmetic, and so not a partial order, which contradicts the initial choice of $\preccurlyeq$.
$R$ is transitive. For suppose that $xRy$ and $yRz$. There are three cases, and in each we will get $xRz$. 1) If $x=y$ then we have $xRz$ from $yRz$ and substitution. 2) If $y=z$ we have $xRz$ from $xRy$ and substitution. 3) Now suppose $x \ne y$ and $y \ne z$. Then by definition of $R$, $y \preccurlyeq x$ and $z \preccurlyeq y$. Because $\preccurlyeq$ is a partial order and hence transitive, and because $z \preccurlyeq y$ and $y \preccurlyeq x$, we have $z \preccurlyeq x$. And so, by definition of $R$, we have $xRz$.
Since $R$ is reflexive, antisymmetric, and transitive, it is by defintion a partial order.
Problem : Let $G$ be a directed graph and define a relation $R$ on the vertices of $G$ by $uRv$ if and only if either $u=v$ or there is a path on which $u$ precedes $v$. Under what conditions is $R$ a partial order?
$R$ is always reflexive since $uRu$ for all vertices $u$ by definition of $R$.
$R$ is always transitive since if $uRv$ and $vRw$, then there is a path on which $u$ precedes $v$; truncate that path to the part that goes from $u$ to $v$. There is also a path on which $u$ precedes $w$; truncate that path to the part that goes from $v$ to $w$. Concatenate the truncated paths to get a path from $u$ to $v$ and then on to $w$; $v$ precedes $w$ on that path and so $uRw$.
So the question becomes "under what conditions is $R$ antisymmetric?" We claim that $R$ is antisymmetric if and only if $G$ is acyclic. $\Rightarrow$ (contrapositive): Suppose that $G$ has a cycle. Pick two distinct vertices $u$ and $v$ on that cycle. The part of the cycle from $u$ to $v$ is a path on which $u$ precedes $v$, so $uRv$. The rest of the cycle is a path from $v$ back to $u$, and $v$ precedes $u$ on that path, so $vRu$. Now we have $uRv$, $vRu$, and $u \ne v$, so $R$ is not antisymmetric. $\Leftarrow$ (contrapositive): Suppose that $R$ is not antisymmetric. Then there are distinct vertices $u$ and $v$ with $uRv$ and $vRu$. By definition of $R$, there are paths $P_1$ and $P_2$ on which $u$ precedes $v$ and $v$ precedes $u$ respectively. Truncate them to the parts from $u$ to $v$ and $v$ to $u$ to get $P'_1$ and $P'_2$, and concatenate those together to get $P$, which is now a path from $u$ to $v$ and back to $u$. $P$ may be a closed walk rather than a cycle, but we can find a shortest subpath of $P$ that starts and ends at the same place (the well-ordering principle!); that subpath is a cycle in $G$, so $G$ is not acyclic.
Problem : Use the definition of $\Theta$ to show that $3x^3-4x^2+10x-5$ is $\Theta(x^3)$.
Also, for $n \ge 5$, we have $4n^2 \le 5n^2 \le n^3$, $10n\ge 0$, and $5 \le n \le n^3$. So for $n \ge 5$ we have \begin{array}{rcl} 3n^3-4n^2+10n-5 & \ge & 3n^3-n^3+10n-n^3 \cr & = & n^3+10n \cr & \ge & n^3. \end{array} We have shown that there exists an $n_0$ (namely 5) and a $c_1$ and $c_2$ (namely 1 and 13 respectively) so that $\forall n \gt n_0, c_1 \cdot n^3 \le 3n^3-4n^2+10n-5 \le c_2 \cdot n^3$. Therefore, by the definition of $\Theta$, $3n^3-4n^2+10n-5 \in \Theta(n^3)$.
Problem : Order the following functions so that if $f$ comes before $g$, then $f$ is of order at most $g$ ($f(n)$ is $O(g(n))$). Indicate which functions can be switched in the lists (in other words, indicate which are of the same order as each other).
- $n \log n$
- $n$
- $2^n$
- $4^n$
- $8n + 1$
- $n^2 + n + 400$
- $n (\log n)^2$
- $n$, $8n + 1$
- $n \log n$
- $n (\log n)^2$
- $n^2 + n + 400$
- $2^n$
- $4^n$